It is known that the expressions 4k+5 and 9k+4 are simultaneously perfect squares for certain natural values of k. What values can the expression 7k+4 attain for the same values of k?

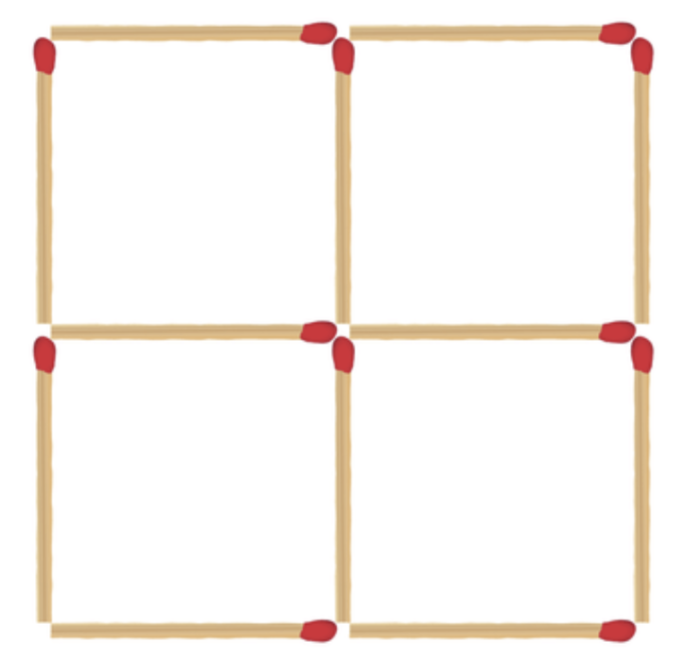
Move 3 matchsticks to get 3 squares. Make sure that after you move or remove matchsticks, there are no dangling matchsticks.

N boys and N girls go out to dance. In how many ways can they all dance (boys must dance with girls)? 💃🏻 🕺🏻

The product of five numbers is not equal to zero.

When you decrease each number by one, the product still stays the same.

Can you give an example of such numbers?

Are there natural numbers x, y and z that satisfy the condition 28x + 30y + 31z = 365?

A three-digit number begins with the number 4. If you move it to the end of the number, you get a number that is 3/4 of the original. Find the original three-digit number.

How many squares are exactly four greater than a prime?

Amrita needs to select a new PIN.

She decides it will be made up of four non-zero digits with the following properties:

i) The first two digits and the last two digits each make up a two-digit number which is a multiple of 11.

ii) The sum of all the digits is a multiple of 11.

How many different possibilities are there for Amrita’s PIN?

Is it possible to arrange the numbers 0, 1 and –1 in a 6x6 table so that all the sums of the numbers along the verticals, horizontals and two main diagonals are different?

There are 28 red, 20 green, 12 yellow, 20 blue, 10 white and 10 black balls in a box.

How many balls need to be randomly drawn from the box, without peeking, to ensure that at least 15 balls of the same color are among those drawn?

With a bag of granulated sugar, a cup scale, and a 1 g weight, is it possible to measure 1 kg of sugar in 10 weighings?

A 1992-digit number is written. Each two-digit number formed by neighbouring digits is divisible by 17 or 23. The last digit is 1. What is the first digit?

What four-digit number is 83 times the sum of its digits?

The arithmetic mean of ten distinct natural numbers is 15. Find the largest value among these numbers.

Each Martian has three hands. Can seven Martians hold hands?

During the first year, the population of a certain village increased by n people, and for the second year, it increased by 300 people. At the same time, over the first year, the population increased by 300%, and for the second year, it increased by n%. How many inhabitants became part of the village?

Is there a numeral system in which 3 + 4 = 10 and 3 × 4 = 15?

What is the base of this system?

Can a 5×5 board be filled with dominoes of size 1×2?

ABCDEF is a six-digit number. All of the digits are different and arranged from left to right in increasing order. The number is a perfect square. Determine what this number is.

Express 203 as the sum of distinct natural numbers whose product is also 203.

‍

Prove that no integer in the sequence 11, 111, 1111, 11111 ... is a perfect square.

‍

All the shapes below are squares. Find the side of the bottom left square if the side of the smallest square is 1.

‍

There are 9 coins, all except one are the same weight, and the odd one is heavier than the rest. You must determine which is the odd one out using an old-fashioned balance. You may use the balance twice. Explain how this can be done.

Can the number 11...11, where there are eighty-one ones, be evenly divided by 81?

The son of the professor's father is talking to the father of the professor's son, but the professor is not participating in the conversation.

Could this be true?

‍